Ingrid Ovans
Professor King
Chemistry 405
29 April 2001
Enzyme Kinetics and Inhibitors
Kinetics is an important part of physical chemistry and enzymes are an important part of biochemistry. Enzyme kinetics is an interesting topic because enzymes are abundant in our bodies and are essentials in our daily lives. One area of emphasis pertaining to enzymes is the study of inhibitors and how they impact kinetics.
If you are given the reaction A + B ® C the rate of this reaction would be determined by the change in the concentration of the reactant or product over a given time interval. If you were using the reactant the sign for the rate would be negative
Rate = -D[A] /D t = -D[B] /D t = D[C] /D t
because you are decreasing the amount of reactant present as the reaction proceeds to the right and of course the opposite is true for the calculation for the product because you would be increasing the amount of product. (Campbell, 150)
Multiplying the reactants raised to their appropriate exponents will give you a value that is proportional to the rate of the reaction.
Rate a [A]a [B]b or Rate = k [A]a [B]b
k is the rate constant and the exponents are values that are determined experimentally. The exponents are usually whole numbers and quite often are the same values as the coefficients of the balanced equations, but not always. The number of molecules involved in the reaction is related to the exponents used to determine the rate. This is the short version of enzyme kinetics. (Campbell, 150)
In 1913 Leoner Michaelis and Maud Menton devised a model to help us better understand the kinetics of enzyme-catalyzed reactions (Campbell, 155). Referring back to the previously mentioned reaction let’s suppose that B ® C where B is the substrate and C is the product. Now if we have that same enzyme being catalyzed by an enzyme the reaction would be A + B Û AB ® A + C where the enzyme is A, AB is the substrate complex and C is the product (Campbell, 156).
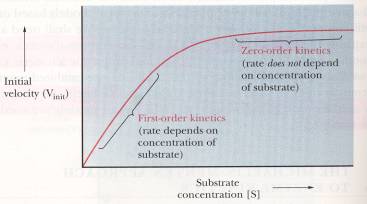
If one were to analyze the rate of this
reaction at varying concentrations of substrate it is found that the rate is
dependent on the concentration of the substrate but this is only true when you
have first-order kinetics (Campbell, 156).
When the reaction is zero-order the rate is independent of the
concentration. This is when the active
sites of the enzyme molecules are saturated (Campbell, 157). Above is a graph that better describes what
is occurring during the first-order kinetics and the zero-order kinetics
(Campbell, 156).
The Vmax is where the reaction proceeds at maximum velocity. KM is where the substrate concentration of the reaction precedes at one half its maximum velocity. A lower KM is preferred because that would mean that there is a higher affinity for the substrate. There is a mathematical relationship between [A], [B], Vmax, and KM. To determine the rate of formation of the enzyme-substrate complex, AB,
Rate of formation = D[AB] / Dt = k1 [A] [B]
where k1 is the rate constant for the formation of the enzyme-substrate complex. After this portion of the reaction things get hairy because you have two things that can occur; the first being the return to the enzyme and substrate and the second the product. After the rate of formation you then have the rate of breakdown for the enzyme-substrate complex, which is
Rate of breakdown = -D[AB] / Dt = k-1 [AB] + k2 [AB]
Where k-1 is the rate constant for the dissociation of the enzyme-substrate complex and k2 is the rate constant for the formation of the product and the release of the enzyme. (Campbell, 157)
Eventually the reaction will reach what is called the steady state where “the rate of formation of the enzyme-substrate complex equals the rate of breakdown.” When the enzyme-substrate complex equals the rate of breakdown it is said that
D[AB] / Dt = -D[AB] / Dt and k1 [A] [B] = k-1 [AB] + k2 [AB]
From there you can substitute values in to calculate the [AB]. (Campbell, 157)
KM, which was mentioned before as the Michaelis constant, is used to solve many different calculations including the enzyme-substrate concentration and the initial rate. These are essential when you want to graph your data. The equation for V is
V = (Vmax [B]) / (KM + [B])
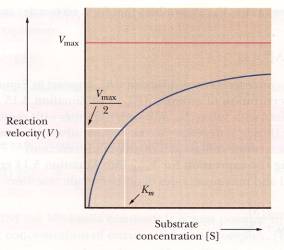
Above is a graph that indicates where Vmax is along with KM (Campbell,
160).
From the equation just mentioned we can derive an equation for a straight line by taking the reciprocals of both sides. Now the equation for a line would be
(1/V) = (KM / Vmax) (1 / [B]) + (1 / Vmax)
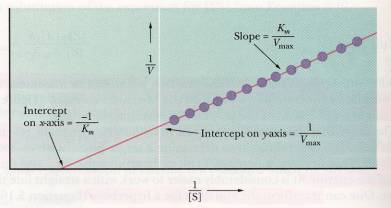
and this of course takes on the form y = mx + b. This is called the Lineweaver-Burk double reciprocal plot of
enzyme kinetics. Along the y-axis is
1/V, the y-intercept is 1 / Vmax
and the slope is KM / Vmax . Upon further investigation you can see that
the x-intercept is = -1/ KM.
This model is useful when dealing with a reversible inhibitor because it
is helpful in determining what kind of inhibitor you are dealing with. Above is
an example of the Lineweaver-Burk double reciprocal plot of enzyme
kinetics. (Campbell, 160)
Understanding the kinetics
behind enzyme substrate binding isn’t the only tool necessary to understanding
this process. Knowing how the substrate
binds to the enzyme will help to understand how an inhibitor binds to an
enzyme. When an enzyme reaction occurs
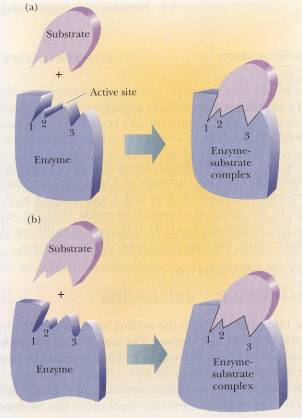
with a catalyst, the enzyme will bind to a substrate (Campbell, 151). A substrate is defined as “a substance that
undergoes an enzyme-catalyzed reaction” (Campbell, 151). The substrate will bind to the active site
in one of two models; the lock-and-key model or the induced-fit model. Above in picture (a) the lock-and-key model
is shown and in (b) the induced-fit model is shown (Campbell, 152). Once the substrate is bound the transition
state is formed, the enzyme-substrate complex (Campbell, 152).
Now knowing how the substrate binds to the enzyme we can explore how inhibitors bind to the enzyme and the kinetics behind them. An inhibitor “is a substance that interferes with the action of an enzyme and slows the rate of a reaction.” There are two kinds of inhibitors: reversible and irreversible. Irreversible inhibitors prevent the original enzyme from ever regenerating. Reversible inhibitors allow the enzyme to release the inhibitor and return to its original state. Within reversible inhibitors there are two categories: competitive and noncompetitive inhibition. (Campbell, 165)
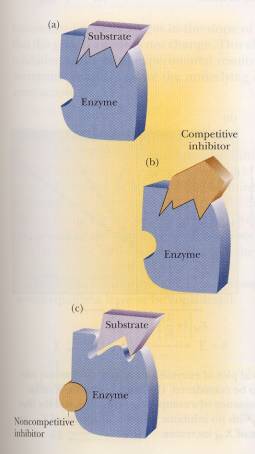
Competitive inhibition is
exactly what it sounds like; the inhibitor competes with the substrate for the
active site preventing the substrate from binding to the enzyme. Noncompetitive inhibition doesn’t compete
with the substrate, but instead binds elsewhere on the enzyme. This binding causes a change in the
structure including the active site, thus preventing the binding to the
substrate. On the previous page there
are diagrams depicting how competitive and noncompetitive inhibitors work. (Campbell, 165)
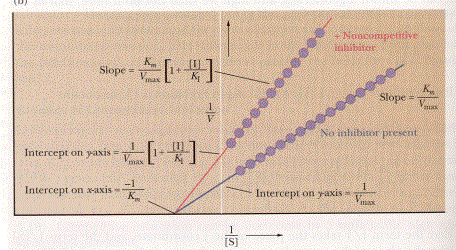
Understanding how they bind is
easy, the kinetics behind them is a little more difficult. As mentioned previously the Lineweaver-Burk
plot is useful for determining what type of inhibitor you are dealing
with. When you have a competitive
inhibitor the Vmax stays unchanged and the KM increases
which can be seen in the graph above (Campbell, 166). As a result, the y-intercept doesn’t change just the slope of the
line will change. When dealing with a
noncompetitive inhibitor the slope also changes for the line along with the
y-intercept, but the x-intercept remains the same, which is depicted on the
previous page (Campbell, 168).
Now that you have background into the kinetics and the binding of inhibitors let us explore some practical applications. If you or someone you know has been infected by the AIDS virus then you would know a lot about the hottest thing on the market for sufferers, protease inhibitors. What are protease inhibitors exactly, they “are drugs that slow down the spread of HIV.” Studies have shown that they are more effective than any of the previously prescribed drugs by reducing the amount of the virus by as much as 99% in certain protease inhibitors. (Markowitz)
To understand how the inhibitor works we need a little background information. In order for HIV to duplicate itself it depends on enzymes. One of the enzymes that is required for this process is the protease enzyme, it is required toward the end of the duplication process. At this point the HIV has entered into the cell wall and made long chains of proteins. But, in order to operate correctly these chains need to be cut into smaller chains and this is the function of the protease enzyme. (Markowitz)
The protease enzyme cuts the long protein chains of the HIV into smaller pieces. The protease inhibitor does exactly what it sounds like it does, it inhibits the protease
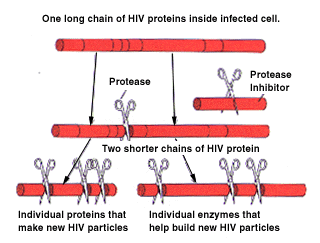
enzyme from cutting the protein chains. The use of this inhibitor reduces the numbers of new infectious HIV. The above diagram shows how the protease works along with its inhibitor. (Markowitz)
Another example that probably most everyone can relate to would be the drug that is prescribed to those that suffer from “depression, panic disorder, obsessive-compulsive disorder (OCD), and posttraumatic stress disorder (PTSD).” The drug for you is sertraline HCl; Zoloft is a product of Pfizer, which is prescribed in over 80 countries. To understand how it works one must begin with a brain chemical called serotonin, which is released from a nerve cell and is then received by the next nerve cell. Some of the serotonin is reabsorbed into the first cell. They believe that not having enough serotonin
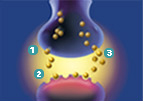
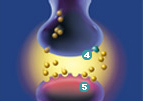
may be associated with the previously mentioned ailments. Above is a picture showing the transfer of the serotonin between the nerve cells. Zoloft works by inhibiting the nerve cell from reabsorbing the serotonin into the first cell. As a result there is an increased amount of serotonin available in the next cell. (Pfizer website)
Cancer is always a hot topic and right now researchers are studying a drug that may get rid of malignant tumors. This drug, called Endostatin, is currently in clinical trials. The drug “specifically inhibits endothelial proliferation and potently inhibits angiogenesis and tumor growth.” The drug had encouraging results on laboratory mice.
There are so many inhibitors that are currently being used and are being developed right now it is hard to keep up. What has been presented is just a taste of what is out there in the world of enzymes and inhibitors so I encourage you to do your own research and find out what is going on in your body. (Endostatin)
Work Cited
Campbell, Mary K. Biochemistry, 3rd ed; Philadelphia: Saunders College Publishing, 1999.
“Endostatin.” http://www.slip.net/~mcdavis/endostat.html
Markowitz MD, Martin. “Protease Inhibitors: What They Are, How They Work, When to Use Them.” http://www.iapac.org/clinmgt/avtherapies/patient/proinbk.html
Pfizer website. “About Zoloft.” http://www.zoloft.com/aboutzoloft.htm